## Points on the Elliptic Curve ### Verify a point on the curve For a given curve, it is easy to verify if a point $G$ lies on it or not. All calculations are done in the $\mathbb{GF(p)}$ for the curve specification. eg: For [secp256k1](https://en.bitcoin.it/wiki/Secp256k1), which is used in bitcoin, $$ y^2 = x^3 + 7 $$ ``` G = ( 6b17 d1f2 e12c 4247 f8bc e6e5 63a4 40f2 7703 7d81 2deb 33a0 f4a1 3945 d898 c296, 4fe3 42e2 fe1a 7f9b 8ee7 eb4a 7c0f 9e16 2bce 3357 6b31 5ece cbb6 4068 37bf 51f5 ) p = ( ffff ffff ffff ffff ffff ffff ffff ffff ffff ffff ffff ffff ffff fffe ffff fc2f ) ``` Let's try to verify if the Generator point $G$ lies on the curve.  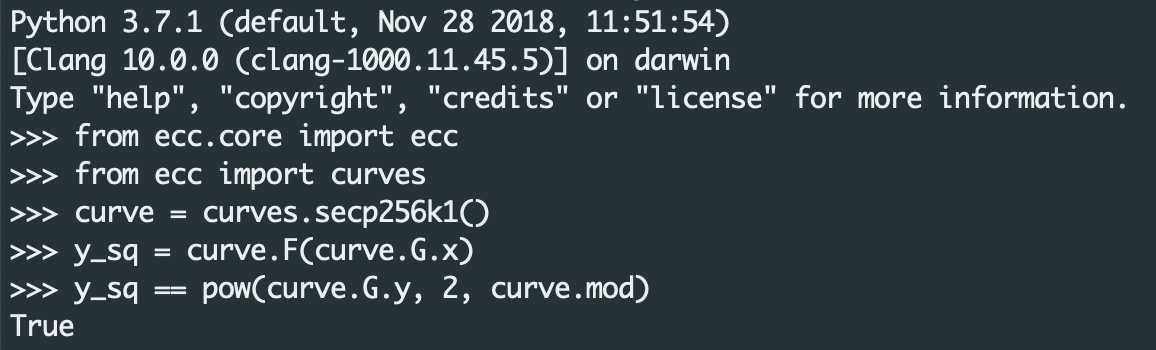The above calculation is to verify if a point $G(x, y)$ lies on the curve. So we calculate $G_x^3 + 7 \pmod{p}$ and $G_y^2 \pmod{p}$. If those are equal, the point lies on the curve. 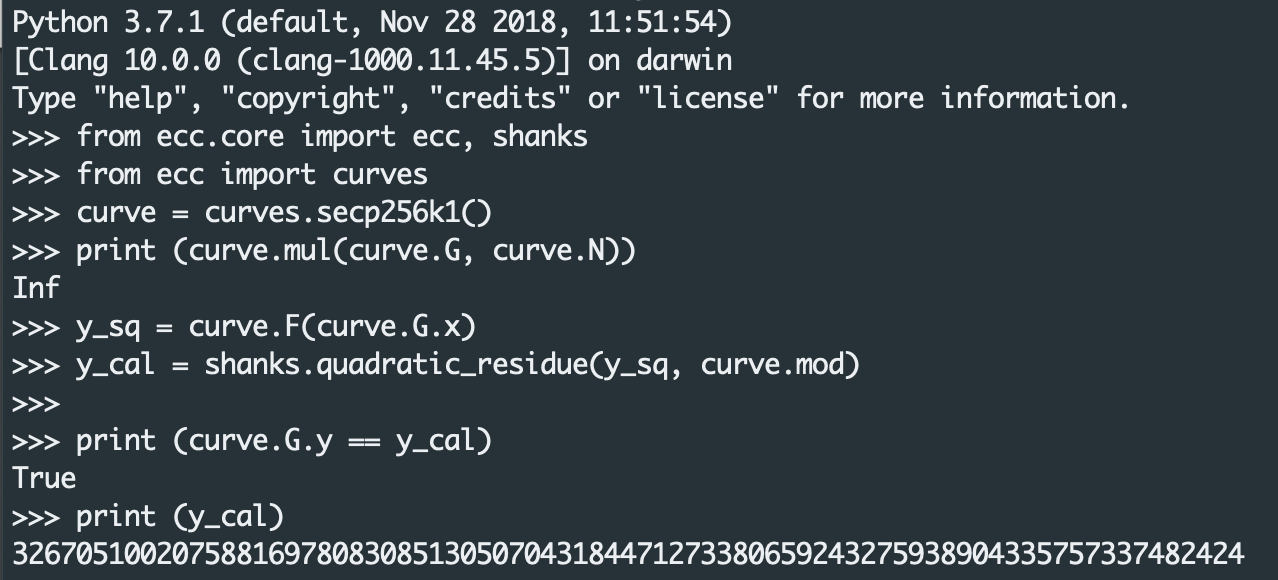### Find $y$ given $x$ on the curve Given a point $x$, we would have to find a $y$. It seems relatively simple, except if this wasn't in $\mathbb{GF(p)}$. If it wasn't on the prime field, we could have done $\pm\sqrt{x^3 + 7}$, but it's not so simple here. To solve this $x^2 \equiv n \pmod{p}$, it's called Quadratic Congruence equations. Here $n$ is called a [Quadratic Residue](https://en.wikipedia.org/wiki/Quadratic_residue) modulo $p$. To do this, we can use the following series of computations. For somewhat detailed explanation, please refer [Solving Quadratic modular equations](quadratic.html).  ---- The scope extends for this topic to * Number of points on the curve or [Order of a curve](https://en.wikipedia.org/wiki/Counting_points_on_elliptic_curves) * Cofactor of a curve * Finding a Generator point on the curve